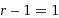Radix Minus One

William John Holden
2014-05-04

1. Introduction
2. Proof
3. Binary
4. Programming
5. Networking
6. Unary

Introduction

Some time ago I noticed an interesting property of binary arithmetic, described in my Math Tricks for IP Subnetting paper, where:

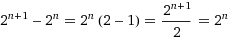
I wondered if such a rule could be applied for any radix. It seems intuitive:

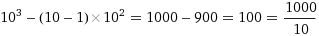
Surprisingly, yes, this is very easily provable, and in binary this gives a very unique property.

Proof

The proof is trivial. For arbitrary radix r we hypothesize:

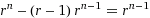
And verify using basic algebra:

Binary

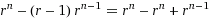
Binary provides several unique properties given 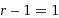, which can be phrased in many ways:

• Subtracting a power of two from the next power of two results in the original power of two:
• Adding a power of two to itself doubles the value (obviously), which happens to increase the power:
• To multiply a binary number by two, just append a zero to the end, just like in decimal we add a zero to the end when multiplying by ten.
• Likewise in division, remove a zero from the tail of a binary number to divide by two.

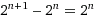
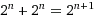
Additional means to express this in spoken language that might suggest further applications.

Programming

This mathematical feature provides a very useful trick for computers: bit shifting. Bit shifting manifests in C-style programming languages as the << and >> operators. These two operators allow a programmer to shift bits to the left or right, which respectively raises or lowers the number by a factor of two equal to the number of shifts shifted.

To multiply an integer value by four, a programmer may use:
x << 2

To divide by sixteen, the programmer could write:
y >> 4

(Note that most programming languages will silently ignore overflows and loss of precision.)

Networking

IT professionals working in networking may also find this property useful when subnetting. Adding or removing a bit to a subnet mask will result in a network that is half or twice the original network size.

To divide a /24 network in half, simply extend the length of the subnet mask by one bit to /25. To divide into four subnets, make /24 into /26. CIDR notation makes this obvious, but it is not as apparent using dotted-decimal subnet masks.

Unary

I might add that this rule does not apply for Unary, where radix r is equal to one, because r-1=0. However, Unary does not have a means to express zero, thus this exception illustrates invalidity of Unary as a number system.