Reindeer Replacements: Solving a children's logic puzzle with OR-Tools

William John Holden

2022-12-18

My daughter brought home this problem from school:

Oh no! Santa's reindeer have come down with the flu, and he has to find some last-minute replacements to pull his sleigh on Christmas Eve. These replacements include dogs, horses, and camels. In order to pull Santa's sleigh, they need to be lined up in the correct order. Use the clues below to help Santa get his reindeer replacements in the correct order.

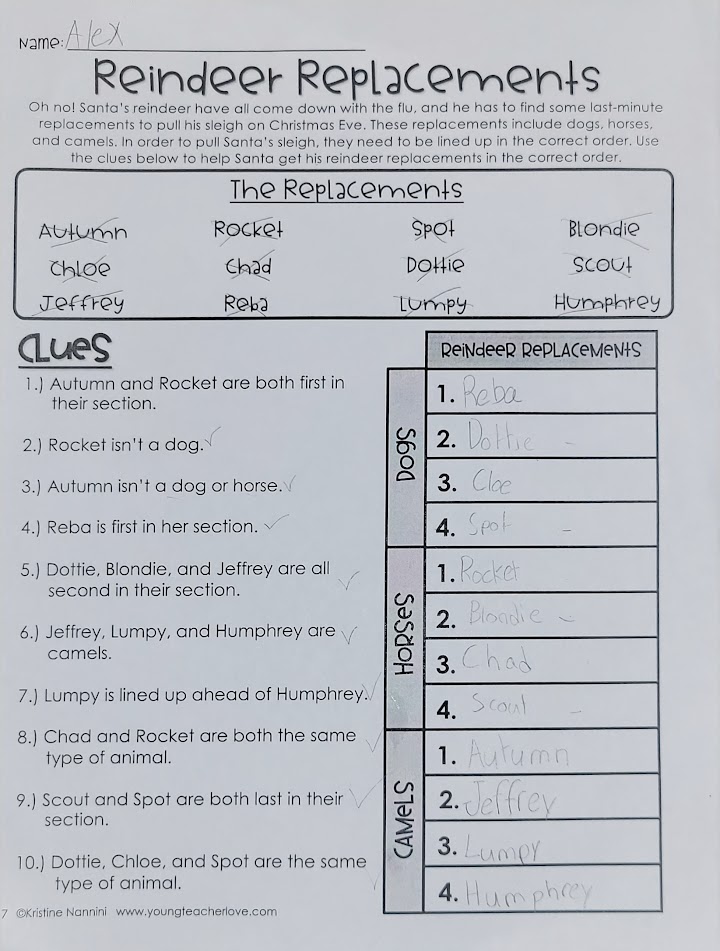
This is a constraint satisfaction problem, and it is a nice opportunity to model a simple problem using sophisticated software. I have been interested in constraint solvers for quite a while. They feel magical and can solve very hard problems, yet they're little-known and seldom-used. I recently got started using Google OR-Tools and used it for a small project for an AI class where I tried to schedule CrossFit workouts.

from IPython.display import YouTubeVideo
YouTubeVideo('rSArqHH0xDI')

Let's use OR-Tools to solve the Reindeer Replacements problem. Constraint solvers can be pretty difficult to use because it is such a different way of programming, so it really helps to read lots of examples. You have to model your problem in a way that the machine can solve, which might be very different from how you would ordinarily visualize the problem.

Search space

We are trying to match a name (Autumn, Rocket, Spot, ...) to a species (dog, horse, or camel) and position (1-4). I like to visualize this kind of problem as a 3D box of points that represents the Cartesian product of our three axes.

We'll model our problem as $12 \times 3 \times 4=144$ Boolean variables. We will stores these variables in a dictionary named V (for variables). Theoretically, there are $2^{144}$ possible assignments of literal values to these variables -- a seemingly intractable problem. In practice, a modern constraint solver will be able to quickly prune the search space and either find some solution or prove that none exists.

replacements = """
Autumn
Rocket
Spot
Blondie
Chloe
Chad
Dottie
Scout
Jeffrey
Reba
Lumpy
Humphrey
""".strip().split("\n")
types = """
Dog
Horse
Camel
""".strip().split("\n")
orders = list(range(1, 5))

We'll need the OR-Tools library and also itertools.product.

from ortools.sat.python import cp_model
import itertools
model = cp_model.CpModel()
V = {}
for (i, j, k) in itertools.product(replacements, types, orders):
    V[(i, j, k)] = model.NewBoolVar('%s is a %s in position number %i' % (i, j, k))

The structure of the problem is that exactly one name goes with each type/order pair.

for i in replacements:
    model.AddExactlyOne(V[(i,j,k)] for (j,k) in itertools.product(types, orders))

Equivalently, each type/order pair relates to exactly one name. I think these constraints are actually redundant because there is a 1:1 relationship with the names and type/order pairs, but the machine does not know that. It often helps the solver to supply additional information. This information may seem like an obvious assumption to you, but it might allow the solver to quickly prune subtrees from its search space. Reducing the search space is a good thing when you're coping with exponential complexity.

for (j,k) in itertools.product(types, orders):
    model.AddExactlyOne(V[(i,j,k)] for i in replacements)

Clues

Autumn and Rocket are both first in their section.

for i in ['Autumn', 'Rocket']:
    model.AddExactlyOne(V[(i, j, 1)] for j in types)

Rocket isn't a dog.

for k in orders:
    model.Add(V[('Rocket', 'Dog', k)] == False)

Autumn isn't a dog or horse.

for (j, k) in itertools.product(['Dog', 'Horse'], orders):
    model.Add(V[('Autumn', j, k)] == False)

Reba is first in her section.

model.AddExactlyOne(V[('Reba', j, 1)] for j in types)

<ortools.sat.python.cp_model.Constraint at 0x2508a1e5af0>

Dottie, Blondie, and Jeffrey are all second in their section.

for i in ['Dottie', 'Blondie', 'Jeffrey']:
    model.AddExactlyOne(V[(i, j, 2)] for j in types)

Jeffrey, Lumpy, and Humphrey are camels.

for i in ['Jeffrey', 'Lumpy', 'Humphrey']:
    model.AddExactlyOne(V[(i, 'Camel', k)] for k in orders)

Lumpy is lined up ahead of Humphrey.

This is tricky to model because the constraint solver does not really know about the position numbers. It just sees true/false variables, so we cannot use a simple position(Lumpy) < position(Humphrey) inequality. We can force it by enumerating implications:

position(Lumpy) = 1 ==> position(Humphrey) = 2, 3, or 4
position(Lumpy) = 2 ==> position(Humphrey) = 3 or 4
position(Lumpy) = 3 ==> position(Humphrey) = 4

for lumpy in range(1, 5):
    model.AddAtLeastOne(V[('Humphrey', 'Camel', humphrey)] for humphrey in range(lumpy + 1, 5)).OnlyEnforceIf(V[('Lumpy', 'Camel', lumpy)])
    print((lumpy, list(range(lumpy + 1, 5))))

(1, [2, 3, 4])
(2, [3, 4])
(3, [4])
(4, [])

Note: there must be a flaw here. I can't get this to work with range(1, 4). I have to instead use range(1, 5). Also, it breaks if I specify AddExactlyOne instead of AddAtLeastOne, but I don't know why.

Chad and Rocket are both the same type of animal.

For this one let's use conditional implication. Let $A$ be the statement "Chad and Rocket are both dogs". If $A$ is true, then we'll enforce a constraint about each of them being dogs. Next, statement $B$ is for horses and statement $C$ for camels.

A = model.NewBoolVar('Chad and Rocket are both dogs')
B = model.NewBoolVar('Chad and Rocket are both horses')
C = model.NewBoolVar('Chad and Rocket are both camels')
model.AddAtLeastOne([A, B, C])
for i in ['Chad', 'Rocket']:
    model.AddAtLeastOne(V[(i, 'Dog', j)] for j in orders).OnlyEnforceIf(A)
    model.AddAtLeastOne(V[(i, 'Horse', j)] for j in orders).OnlyEnforceIf(B)
    model.AddAtLeastOne(V[(i, 'Camel', j)] for j in orders).OnlyEnforceIf(C)

Here, again, I'm having trouble with AddExactlyOne and have had to use AddAtLeastOne instead.

Scout and Spot are both last in their section.

for i in ['Scout', 'Spot']:
    model.AddExactlyOne(V[(i, j, 4)] for j in types)

Dottie, Chloe, and Spot are the same type of animal.

We can use the same implication strategy that we used earlier for Chad and Rocket.

D = model.NewBoolVar('Dottie, Chloe, and Spot are all dogs')
E = model.NewBoolVar('Dottie, Chloe, and Spot are all horses')
F = model.NewBoolVar('Dottie, Chloe, and Spot are all camels')
model.AddExactlyOne([D, E, F])
for i in ['Dottie', 'Chloe', 'Spot']:
    model.AddAtLeastOne(V[(i, 'Dog', j)] for j in orders).OnlyEnforceIf(D)
    model.AddAtLeastOne(V[(i, 'Horse', j)] for j in orders).OnlyEnforceIf(E)
    model.AddAtLeastOne(V[(i, 'Camel', j)] for j in orders).OnlyEnforceIf(F)

Solution

solver = cp_model.CpSolver()
status = solver.Solve(model)
status == cp_model.OPTIMAL or status == cp_model.FEASIBLE

True

solution = ["%s #%d: %s" % (j, k, i) for (j, k, i) in itertools.product(types, orders, replacements) if solver.Value(V[(i,j,k)])]
solution

['Dog #1: Reba',
 'Dog #2: Dottie',
 'Dog #3: Chloe',
 'Dog #4: Spot',
 'Horse #1: Rocket',
 'Horse #2: Blondie',
 'Horse #3: Chad',
 'Horse #4: Scout',
 'Camel #1: Autumn',
 'Camel #2: Jeffrey',
 'Camel #3: Lumpy',
 'Camel #4: Humphrey']